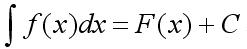
Интеграл — математический синоним суммы последовательности. Процесс решения интеграла называется интегрированием. Интегрирование — это операция обратная диференционированию. Иными словами, если взять производную от функции, которая получится в результате интегрирования, её результатом будет исходный интеграл. Если интеграл неопределенный, достаточно взять первообразную от подынтегральной функции:
Определенный интеграл решается по формуле Ньютона-Лейбница:

Основные первообразные для простых интегралов давно собраны в таблицу интегралов, полный вариант которой несложно найти в любом математическом учебнике.
Если же данные теоретические выкладки не дали вам понимания, как решать интегралы, вы можете воспользоваться онлайн сервисами для упрощения этой задачи:
1) http://kontrolnaya-rabota.ru/s/integral/
2) http://www.wolframalpha.com/
(Важно!) Рассмотрена самая простая разновидность интеграла. Существуют также кратные, криволинейные, поверхностные и другие типы интегралов, решение которых весьма не очевидно и может изменяться в зависимости от конкретного рассмотренного случая.